Question

A quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB + CD = AD + BC

A quadrilateral is drawn to circumscribe a circle. Prove that the sum of opposite sides are equal.

Answer 1

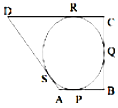
We know that the tangents drawn from an external point to circle are equal..

∴ AP = AS  .........(i)  [tangents from A]

BP = BQ   .....(ii)  [tangents from B]

CR = CQ  .......(iii) [tangents from C]

DR = DS  .......(iv)  [tangents from D]

∴ AB + CD = (AP + BP) + (CR + DR)

= (AS + BQ) + (CQ + DS)

[using (i), (ii), (iii) and (iv)]

= (AS + DS) + (BQ + CQ)

= AD + BC

Hence, (AB + CD) = (AD + BC)