Given that the lines are 3x - 4y + 4 = 0 and 6x - 8y - 7 = 0 are the tangents to the circle.

Let us find the slope of each line.
We know that the slope of the line ax + by + c = 0 is \(\frac{-b}a\).
⇒ The slope of the line 3x - 4y + 4 = 0 is \(\frac{-(-4)}3=\frac43\)
⇒ The slope of the line 6x - 8y - 7 = 0 is \(\frac{-(-8)}6=\frac43\)
The slopes are equal. So, these are the tangents on either side of the diameter of the circle as shown in the figure.
The length of the diameter is the perpendicular distance between these two parallel lines.
We know that the distance between the two parallel lines ax + by + c1 = 0 and ax + by + c2 = 0 is given by
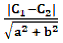
Here the parallel are 3x - 4y + 4 = 0 and 6x - 8y - 7 = 0 (or 3x - 4y - \(\frac72\)= 0)
Let ‘d’ and ‘r’ be the diameter and radius of the circle.
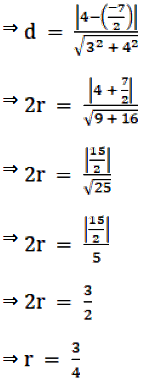
∴ The radius of the circle is \(\frac34\) units.