Question

The equation of the circle which touches the axes of coordinates and the line x/3 + y/4 = 1 and whose centres lie in the first quadrant is x² + y²- 2cx - 2cy + c² = 0, where c is equal to

A. 4

B. 2

C. 3

D. 6

Answer 1

Correct option is D. 6

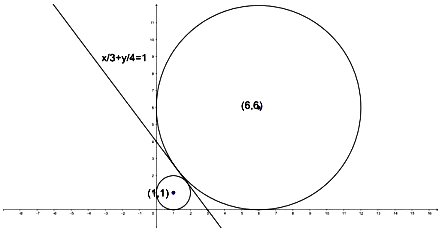
Given that the equation of the circle which touches the axes of coordinates and the line \(\frac {\text x}3+\frac{y}3=1\) and whose centres lie in the first quadrant is x² + y² - 2cx - 2cy + c² = 0. We need to find the value of c.

We know that for a circle x² + y² + 2ax + 2by + c = 0

⇒ Centre = (- a, - b)

⇒ Radius = \(\sqrt{a^2+b^2-c}\)

For x² + y² - 2cx - 2cy + c² = 0

We have \(\frac {\text x}3+\frac{y}3=1\) touching the circle.

We know that the perpendicular distance between the circle and centre is equal to the radius of the circle.

We know that the perpendicular distance between from the point (x₁, y₁) to the line ax + by + c = 0 is

⇒ c² - 7c + 6 = 0

⇒ c² - 6c - c + 6 = 0

⇒ c(c - 6) - 1(c - 6) = 0

⇒ (c - 1)(c - 6) = 0

⇒ c - 1 = 0 or c - 6 = 0

⇒ c = 1 or c = 6