As we need to find \(\lim\limits_{\text x \to0}\cfrac{\sqrt{1+\text x}-1}{log(1+\text x)} \)
lim(x→0) (√(1 + x) - 1)/(log(1 + x))
We can directly find the limiting value of a function by putting the value of the variable at which the limiting value is asked if it does not take any indeterminate form (0/0 or ∞/∞ or ∞-∞, .. etc.)
Let Z = \(\lim\limits_{\text x \to0}\cfrac{\sqrt{1+\text x}-1}{log(1+\text x)} \)
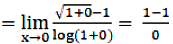
\(=\cfrac00\)(indeterminate)
∴ We need to take steps to remove this form so that we can get a finite value.
TIP: Most of the problems of logarithmic and exponential limits are solved using the formula
\(\lim\limits_{\text x \to0}\cfrac{a^{\text x-1}}{\text x}\) = log a and \(\lim\limits_{\text x \to0}\cfrac{log(1+\text x)}{\text x}=1\)
As Z = \(\lim\limits_{\text x \to0}\cfrac{\sqrt{1+\text x}-1}{log(1+\text x)} \)
To apply the formula of logarithmic limits we need to get the form that matches with one in formula
∴ multiplying numerator and denominator by \(\sqrt{1+\text x}+1\)

{using (a + b)(a - b) = a2- b2}

Use the formula: \(\lim\limits_{\text x \to0}\cfrac{log(1+\text x)}{\text x}=1\)
\(\therefore\) Z = 1/2
Hence,
