If y = √(tan x+√(tan x + √(tan x + .....∞ ))), prove that dy/dx = sec^2 x/(2y - 1)

Question

If y = \(\sqrt{tan\,\text x+\sqrt{tan\,\text x+\sqrt{tan\,\text x....\infty}}}\), prove that dy/dx = \(\cfrac{sec^2\text x}{(2y-1)}.\)

√(tan x+√(tan x + √(tan x + .....∞ ))), sec² x/(2y - 1)

Answer 1

Given: y = \(\sqrt{tan\,\text x+\sqrt{tan\,\text x+\sqrt{tan\,\text x....\infty}}}\),

To prove : dy/dx = \(\cfrac{sec^2\text x}{(2y-1)}.\)

√(tan x+√(tan x + √(tan x + .....∞ ))), sec² x/(2y - 1)

Formula used : log a = log b^m 

log a = m log b

If u and v are functions of x, then

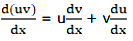
The CHAIN RULE states that the derivative of f(g(x)) is f’(g(x)).g’(x)

y = \(\sqrt{tan\,\text x+y}\)

squaring on both sides

y² = tan x + y

Differentiating with respect to x