Answer is : C. 2
Given: x > 0 and xy = 1
We need to find the minimum value of (x + y).
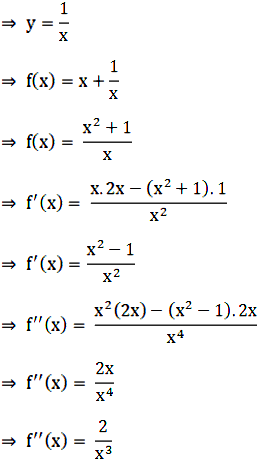
For maximum or minimum value f’(x) = 0.
∴ \(\frac{x^2-1}{x^2}\) = 0
∴ x = 1 or x = -1
f’’(x) at x = 1.
∴ f’’(x) = 2.
F’’(x) > 0 it is decreasing and has minimum value at x = 1
At x = -1
f’’(x) = -2
f’’(x) < 0 it is increasing and has maximum value at x = -1.
∴ Substituting x = 1 in f(x) we get
f(x) = 2.
∴ The minimum value of given function is 2.