Find the general solution for differential equations. x dy\dx - y = 2x^2 sec x

Question

Find the general solution for \(x \frac{dy}{dx} \) - y = 2x² sec x differential equations.

x dy\dx - y = 2x² sec x

Answer 1

Given Differential Equation :

\(x\frac {dy}{dx} \) - y = 2x² sec x

Formula :

i) \(\int\) cot x dx = log (sin x)

ii) alog b = log b^a 

iii) a^{log_a b} = b

iv) \(\int\) xⁿ dx = \(\frac{x^{n+1}}{n+1}\)

v) General solution :

For the differential equation in the form of

\(\frac{dy}{dx} \, +\, Py = Q\)

For the differential equation in the form of

y. (I.F.) = \(\int\) Q. (I.F.) dx + c

Where, integrating factor,

I.F. = \(e^{\int p\, dx}\)

Given differential equation is

\(x \frac{dy}{dx}\) - y = 2x² sec x ……eq(1)

Dividing above equation by x,

∴ \(\frac{dy}{dx} \, - \frac{1}{x}\) y 2x sec x

Equation (1) is of the form

\(\frac{dy}{dx} \, + Py\, =Q\)

Where, P = \(\frac{-1}{x}\) and Q = 2x sec x

Therefore, integrating factor is

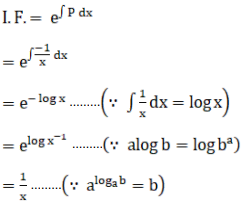
General solution is

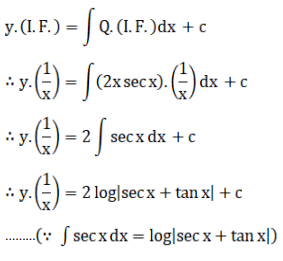
Multiplying above equation by x,

∴ y = 2x log |sec x + tan x| + cx

Therefore, general solution is

y = 2x log |sec x + tan x| + cx