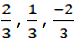Given : A vector \((2\hat i+\hat j-2\hat k)\)
(2i + j - 2k)
To find : Direction cosines of the vector
Formula used : If a vector is \(l\vec i+m\vec j+n\vec k\) then direction cosines are given by \(\cfrac{1}{\sqrt{l^2+m^2+n^2}}\), \(\cfrac{m}{\sqrt{l^2+m^2+n^2}}\), \(\cfrac{n}{\sqrt{l^2+m^2+n^2}}\)
Here l = 2 , m = 1 , n = -2
Direction cosines of the line with direction ratios 2, 1, -2 is
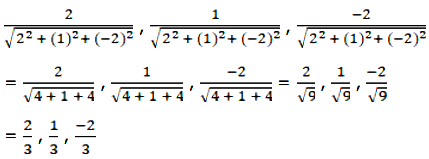
Direction cosines of the vector is