Evaluate the following integrals: ∫ ((log x)/(1 + log x)^2) dx

Question

Evaluate the following integrals:

\(\int \frac{log\,x}{(1 + log\, x)^2}dx\)

∫ ((log x)/(1 + log x)²) dx

Answer 1

 

∫ ((log x)/(1 + log x)²) dx

⇒ log x = A (1 + log x) + B

For x = 1, equation: 0 = A + B

For x = 1/e, equation: -1 = B i.e. B = -1

So, A = 1

Tip – If f₁(x) and f₂(x) are two functions , then an integral of the form ∫ f₁(x)f₂(x)dx can be INTEGRATED BY PARTS as

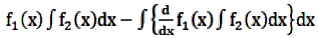
where f₁(x) and f₂(x) are the first and second functions respectively.

Taking f₁(x) = 1/(1 + log x) and f₂(x) = 1in the second integral and keeping the first integral intact,

where c is the integrating constant.