Analogous Systems
Let us consider a mechanical (both translational and rotational) and electrical system as shown in the fig.
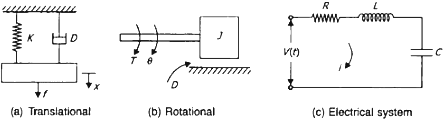
From the fig (a)
M\(\frac{d^2x}{dt^2}\) + D\(\frac{dx}{dt}\)+ Kx = F .....(1)
We get (1) From the fig (b)
f \(\frac{d^2θ}{dt^2}\) + D\(\frac{dθ}{dt}\)+ kθ = T ....(2)
We get (2) From the fig (c)
L\(\frac{d^2q}{dt^2}\) + D\(\frac{dq}{dt}\)+ q\(\frac{1}{C}\) = v(t) ....(3)
Where q = fidt
They are two methods to get analogous system.
These are
(i) force- voltage (f-v) analogy and
(ii) forcecurrent (f-c) analogy
(i) Force –Voltage (f-v) Analogy
| Translational |
Electrical |
Rotational |
| Force (F) |
Voltage (V) |
Torque (T) |
| Mass (M) |
Inductance (L) |
Inertia (J) |
| Damper (D) |
Resistance (R) |
Damper (D) |
| Spring (K) |
Elastance (1/C) |
Spring (K) |
| Displacement (x) |
Charge (q) |
Displacement (θ) |
| Velocity (u) |
Current (I) |
Velocity (ω) |
(ii) Force – Current (f-c) Analogy
| Translational |
Electrical |
Rotational |
| Force (F) |
Current (I) |
Torque (T) |
| Mass (M) |
Capacitance (C) |
Inertia (J) |
| Damper (D) |
Reciprocal of Inductance (1/L) |
Damper (D) |
| Spring (K) |
Conductance (1/K) |
Spring (K) |
| Displacement (x) |
Flux Linkage (ψ) |
Displacement (θ) |
| Velocity \(\Big(u-\frac{dx}{dt}\Big)\) |
Velocity \(\Big(v-\frac{dψ}{dt}\Big)\) |
Velocity \(\Big(\frac{dθ}{dt}\Big)\) |