Question

Obtain an expression relating the torque with angular acceleration for a rigid body.

Answer 1

A torque acting on a body produces angular acceleration. Consider a rigid body rotating about an axis passing through the point O and perpendicular to the plane of the figure. Suppose that a torque \(\vec\tau\) on

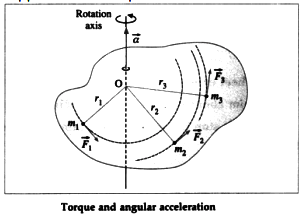
the body produces uniform angular acceleration \(\vec\alpha\) along the axis of rotation. The body can be considered as made up of N particles with masses m₁ , m₂ , …, m_N situated at perpendicular distances r₁ , r₂ , …, r_N respectively from the axis of rotation \(\vec\alpha\) , is the same for all the particles as the body is rigid. Let \(\vec F_1\), \(\vec F_2\) , …, \(\vec F_N\) be the external forces on the particles.

The torque  \(\vec \tau_1\), on the particle of mass m₁ , is 

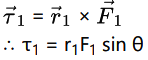
where θ is the smaller of the two angles between \(\vec r_1\) and \(\vec F_1\).

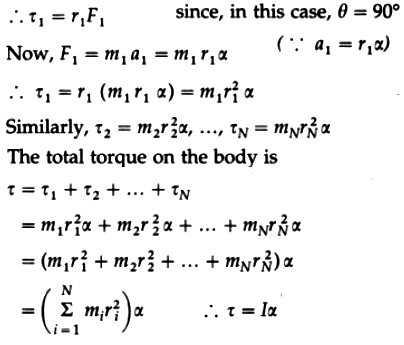
where

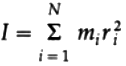
is the moment of inertia of the body about the axis of rotation.

In vector form, \(\vec\tau = I\vec\alpha\) This gives the required relation. Angular acceleration \(\vec\alpha\) has the same direction as the torque \(\vec\tau\) and both of them are axial vectors along the rotation axis.