Question

A particle is projected from the ground at `t = 0` so that on its way it just clears two vertical walls of equal height on the ground. The particle was projected with initial velocity `u` and at angle `theta` with the horiozontal. If the particle passes just grazing top of the wall at time `t = t_1 and t = t_2`, then calculate.
(a) the height of the wall.
(b) the time `t_1 and t_2` in terms of height of the wall.
Write the expression for calculating the range of this projectile and separation between the walls.

Answer 1

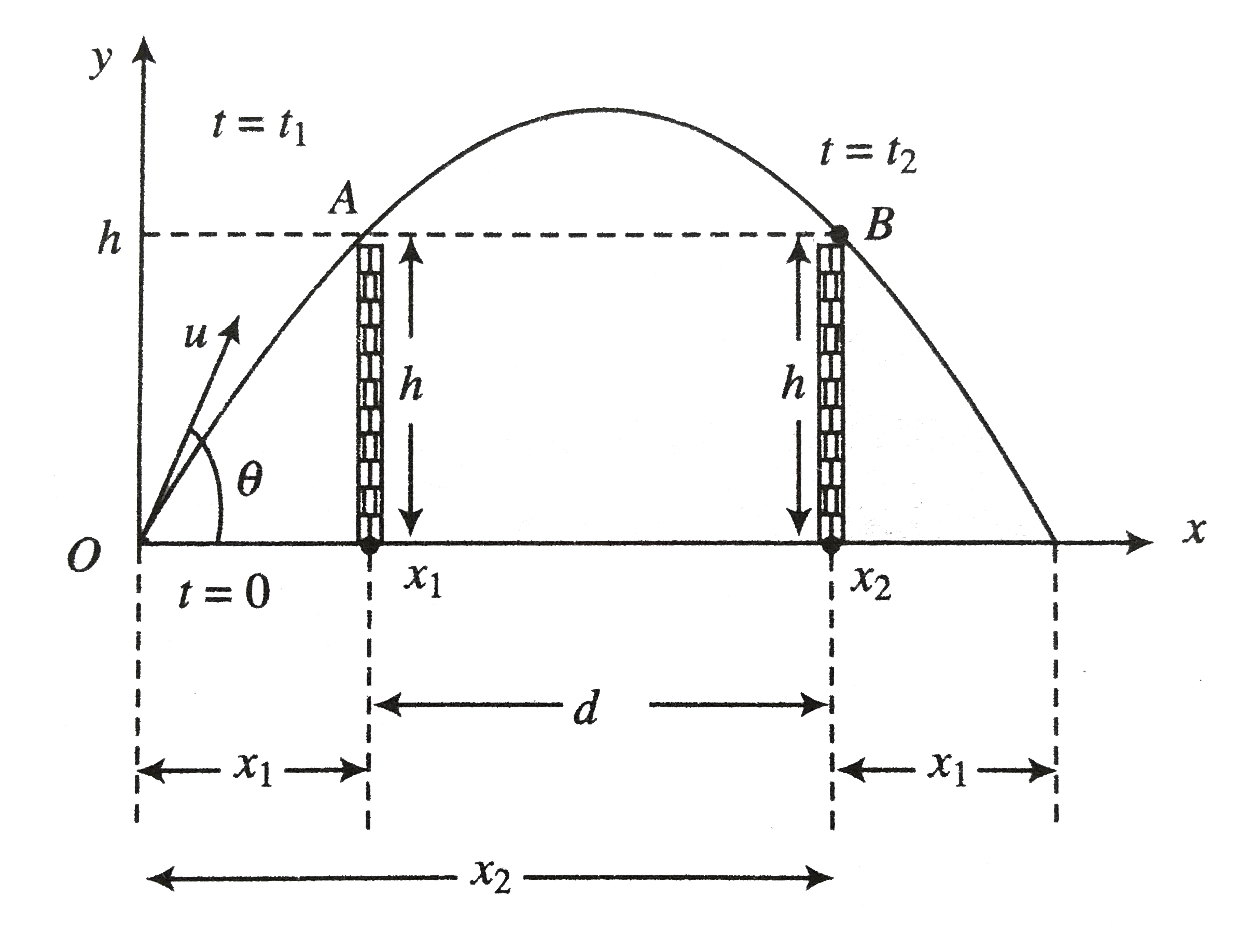
`h = (u sin theta) t_1 - (1)/(2) "gt"_1^2` ….(i)
and `h = (u sin theta) t_2 - (1)/(2) "gt"_2^2` …(ii)
Comparing equation (i) with equation (ii)
`u sin theta = (g(t_1 + t_2))/(2)`
Substituting this value in equation (i), we get
`h = g((t_1 + t_2)/(2)) t_1 - (1)/(2) "gt"_1^2 rArr h = ("gt"_1 t_2)/(2)`
Time `(t_1 and t_2) : h u sin theta t - (1)/(2) "gt"^2`
`t^2 -(2 u sin theta)/(g) t + (2 h)/(g) = 0`
Solving for `t`, we get
`t_1 = (u sin theta)/(g) [1 + sqrt(1 + (sqrt((2 g h)/(u sin theta)))^2)]`
and `t_2 = (u sin theta)/(g) [1 -(sqrt((2 g h)/(u sin theta)))^2]`.
.