Question

A point mass of 1kg collides elastically with a stationary point mass of 5 kg. After their collision, the 1kg mass reverses its direction and moves with a speed of `2ms^-1`. Which of the following statements (s) is (are) correct for the system of these two masses?
A. Total momentum of the system is `3 kg ms^(-1)`
B. Momentum of `5 kg` mass after collision is `4 kg ms^(-1)`
C. Kinetic energy of the centre of mass is `0.75 J`
D. Total kinetic energy of the system is `4 J`

Answer 1

Correct Answer - A::C
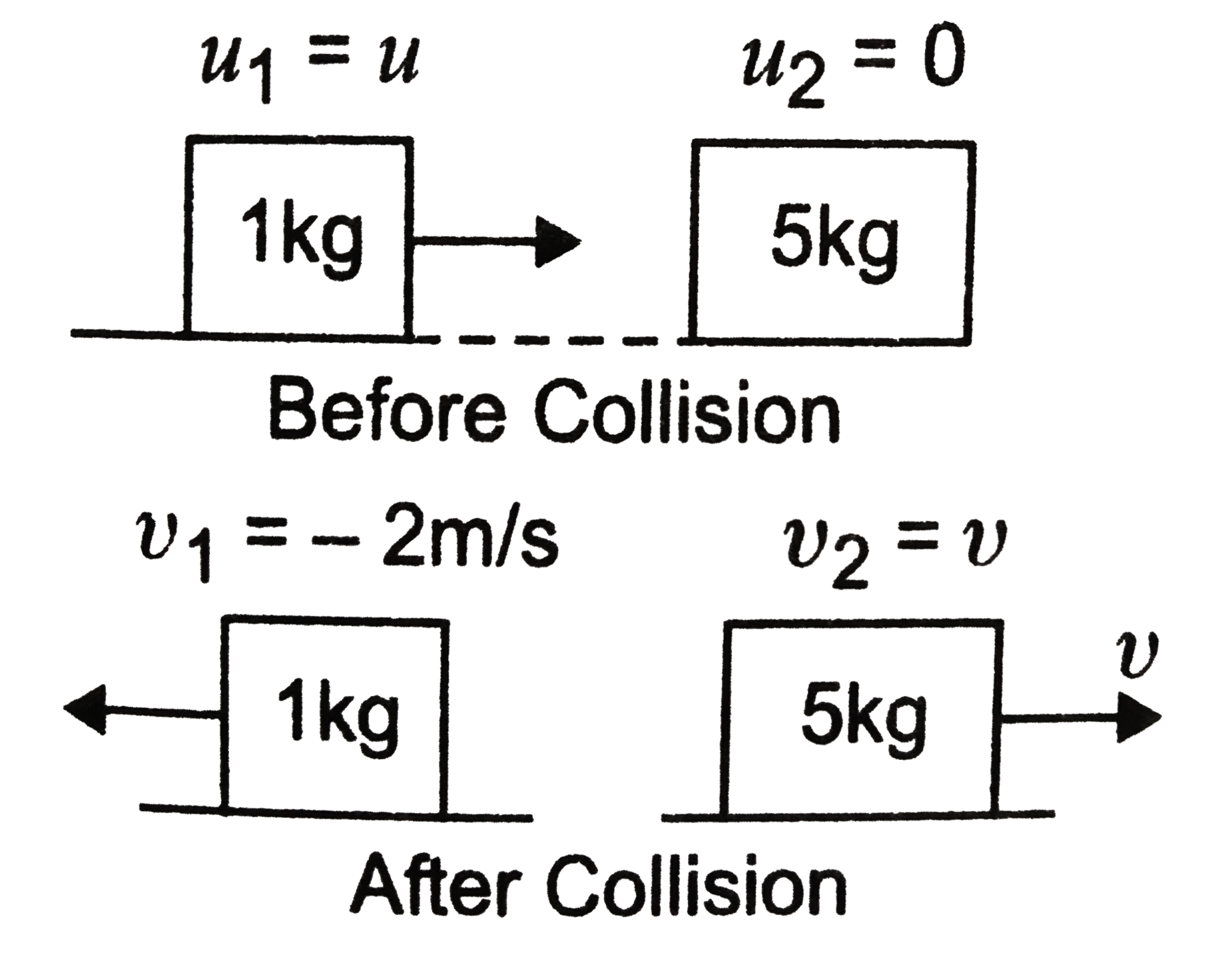
Total momentum before collision
`=m_(1)u_(1)+m_(2)u_(2)=1xxu+5xx0= u `
Total momentum after collision
`= m _(1) upsilon_(1)+ m_(2)upsilon_(2)=1xx(-2)=5 xxupsilon`
`=5 upsilon-2`
According to law of conservation of linear momentum
`u=5 upsilon-2 ...(i)`
Accroding to law of conservation of `K.E.`
`(1)/(2)m_(1)u_(1)^(2)+(1)/(2) m_(2)u_(2)^(2)=(1)/(2)m_(1)upsilon_(1)^(2)+(1)/(2)m_(2) upsilon_(2)^(2)`
or `(1)/(2) xx1xxu^(2)+(1)/(2)xx5xx0=(1)/(2)xx1xx(-2)^(2)+(1)/(2)xx5 upsilon^(2)`
or `u^(2)=4+5upsilon^(2) ...(ii)`
Solving `(i)` and `(ii)`, we get `upsilon=1 m//s`
and `u=3m//s`
Total momentum of the system before collision
`=3 kg m//s.`
Momentum of `5 kg` mass after collision `= m_(2)upsilon_(2)`
`=5xx1=5kg ms^(-1)`
Now,`upsilon_(cm)=(m_(1)upsilon_(1)+m_(2)upsilon_(2))/(m_(1)+m_(2))`
`=(1(-2)+5(1))/(1+5)=(1)/(2) m//s`
`K.E.` of `c.m=(1)/(2)(m_(1)+m_(2))upsilon_(cm)^(2)`
`=(1)/(2) (1+5)((1)/(2))^(2)=0.75J`
Total `K.E.` of the system `=(1)/(2) m_(1)upsilon_(1)^(2)+(1)/(2) m_(2)upsilon_(2)^(2)`
`=(1)/(2)xx1xx(-2)^(2)+(1)/(2)xx5xx1^(2)=2+2.5=4.5J.`