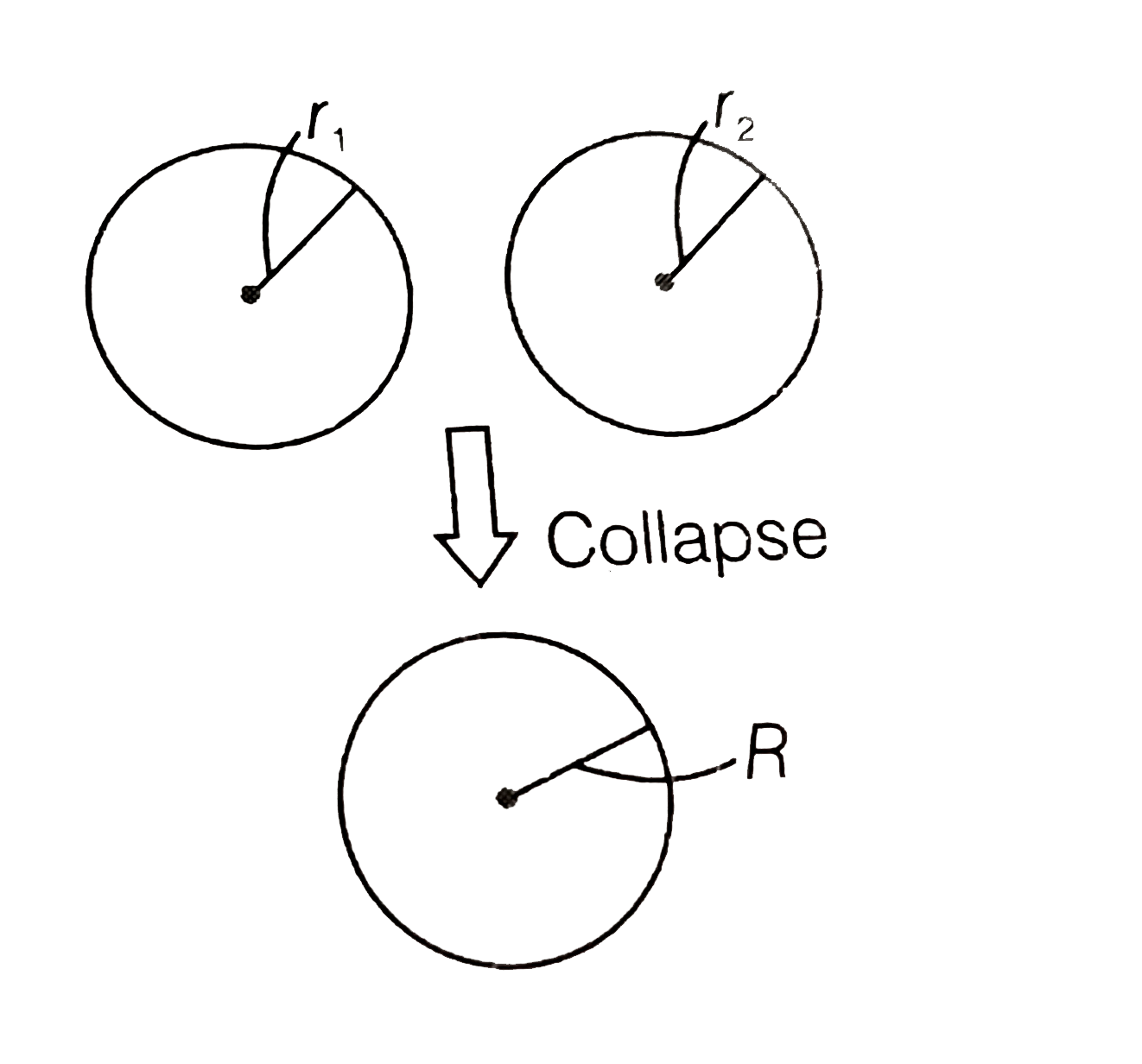Question

Two mercury droplets of radii 0.1 cm and 0.2 cm collapse into one single drop. What amount of energy is released? The surface tension of mercury `T = 435. 5xx10^(-3) Nm^(-1)`

Answer 1

Consider the diagram
Radii of mercury droplets `r_(1)=0.1 cm =1xx10^(-3)`m
`" "r_(2)=0.2 cm =2xx10^(-3)` m
Surface tension (T) `=435.5 xx 10^(-3)` N/m
Let the radius of the big drop formed by collapsing be R.
`therefore` Volume of big drop=Volume of small droplets
`(4)/(3)piR^(3)=(4)/(3)pir_(1)^(3)+(4)/(3)pir_(2)^(2)`
or `R^(3)=r_(1)^(3)+r_(2)^(3)`
` =(0.1)^(3)+(0.2)^(3)`
`=0.001+0.008`
`=0.009`
or `R=0.21 cm =2.1xx10^(-3) m`
`therefore` change in surface area `DeltaA=4piR^(2)-(4pir_(1)^(2)+4pir_(2)^(2))`
`=4pi[R^(2)-(r_(1)^(2)+r_(2)^(2))]`
`therefore` Energy released `=Tdot DeltaA" "` (where T is surface tension of mercury)
`=Txx4pi[R^(2)-(r_(1)^(2)+r_(2)^(2))]`
`=435.5xx10^(-3)xx4xx3.14[(2.1xx10^(-3))^(2)-(1xx10^(-6)+4xx10^(-6))]`
`=435.5xx4xx3.14[4.41-5]xx10^(-6)xx10^(-3)`
`=-32.23xx10^(-7)" "` (Negative sign shows absorption)
Therefore, `3.22xx10^(-6)` J energy will be absorbed.
Note In this process, energy is not conserved . Energy is 1st due to the collapsing in the form of radiations.