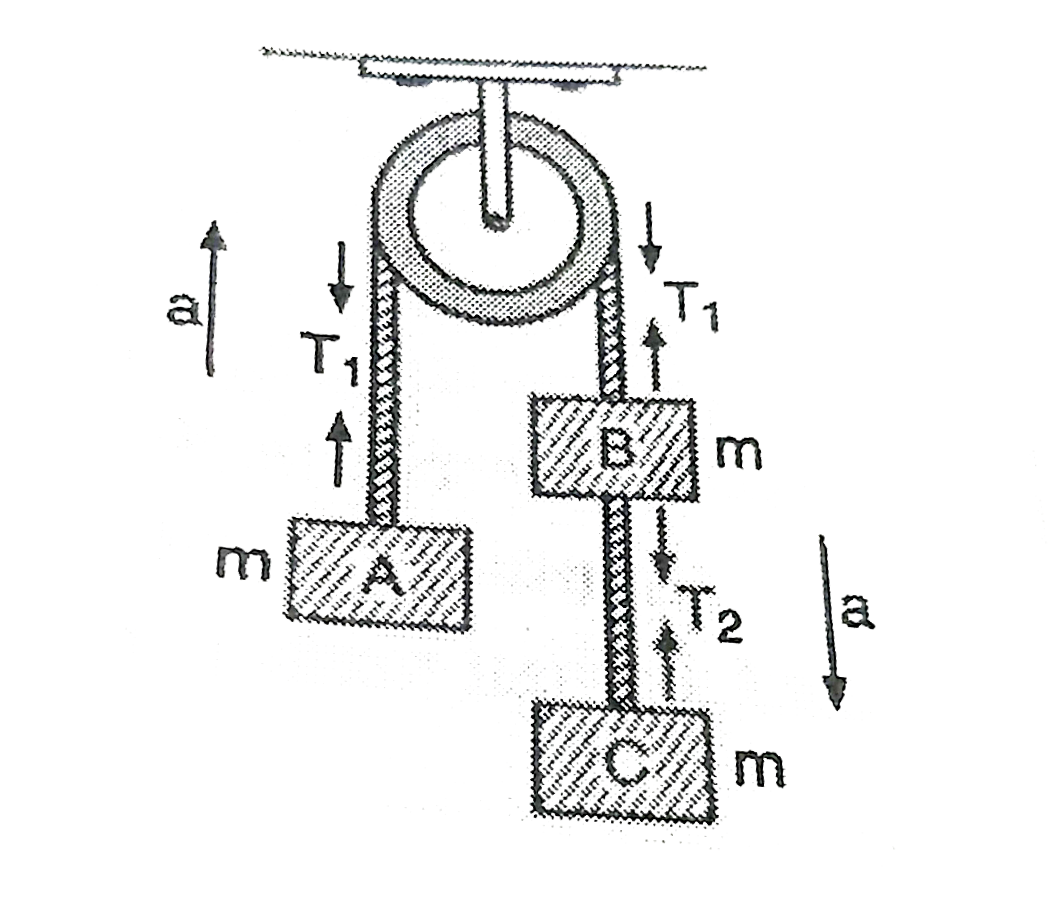Question

Three equal weights of mass m each are hanging on a string passing over a fixed pulley as shown in fig. The tensions in the string connecting weights A to B and B to C will respectively be -

Answer 1

In this problem, as the pulling force is 2mg while opposing force is mg, so net force `=2mg-mg=mg` and as the mass in motion `=m+m+m=3m`
So, the acceleration `=("force")/("Mass")=(mg)/(3m)=g/3`
Now as A is accelerating up while B and C down, so tension `T_(1)` is such that
`mg lt T_(1) lt 2mg`
Actually for the motion of A
`T_(1)=m(g+a)=m(g+g//3)`
`=(4//3)mg`
Now to calculate tension in the string BC we consider the downward motion of C,
i.e., `T_(2)=m(g-a)=m(g-g//3)=(2//3)mg`