Question

The electric field due to uniformly charged sphere of radius `R` as a function of the distance from its centre is represented graphically by
A.
B.
C.
D.

Answer 1

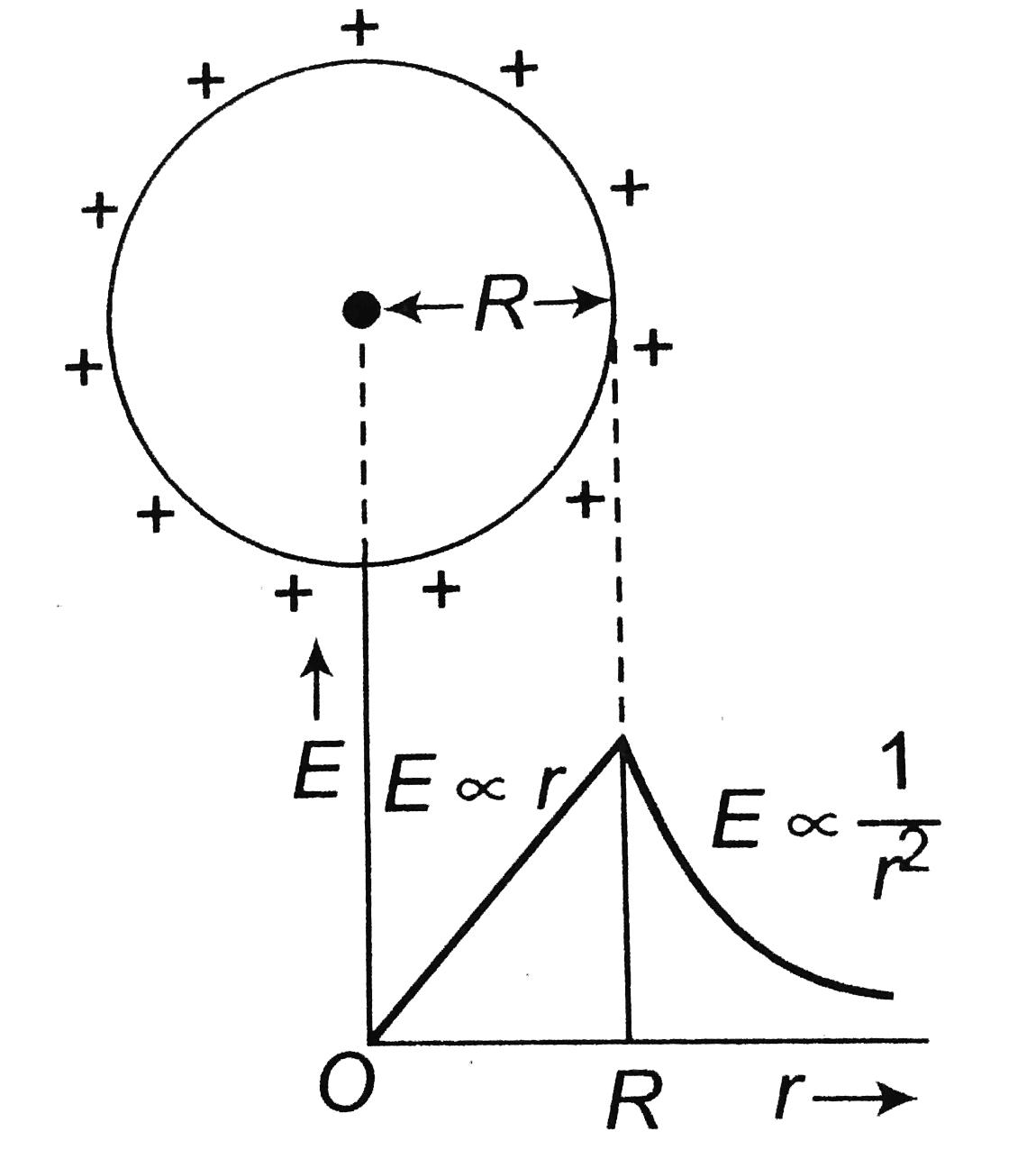
Correct Answer - b
`E_("inside")=(rho)/(3epsilon_(0))r " " (r lt R)`
`E_("outside") = (rho R^(3))/(3 epsilon_(0) r^(2)) " "(r ge R)`
i.e., inside the uniformly charged sphere field varies linearly `(E prop r)` with distance and outside varies according to `E prop (1)/(r^(2))`
Aliter: Outside the spherical charge, the intensity of electric field at a distance `r` from the centre of the charge, `E= (1)/(4pi epsilon_(0)) (q)/(r^(2)) " " (if r gt R)`
On the surface of spherical charge,
`E=(1)/(4piepsilon_(0))(qr)/(R^(3)) " " (if r lt R)`