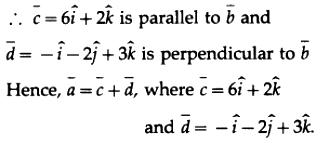Let \(\overline{a} = \overline{c} + \overline{d},\) where \(\overline{c}\) is parallel to \(\overline{b}\) and \(\overline{d}\) is perpendicular to \(\overline{b}\).
Since, \(\overline{c}\) is parallel to \(\overline{b}, \overline{c} = m \overline{b},\) where m is a scalar.
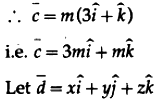
Since, \(\overline{d}\) is perpendicular to \(\overline{b}\) = \(3\hat{i} + \hat{k}, \) \(\overline{d}\) . \(\overline{b}\) = 0

By equality of vectors
3m + x = 5 … (1)
y = -2
and m – 3x = 5
From (1) and (2)
3m + x = m – 3x
∴ 2m = -4x m
∴ m = -2x
Substituting m = -2x in (1), we get
∴ -6x + x = 5
∴ -5x = 5
∴ x = -1
∴ m = -2x = 2