а§ѓа§єа§Ња§Б `Sigma _(1 ) ` ৪১৺ ৙а§∞ а§Ъа§Ња§∞ а§ђа§ња§В৶а•Б P , Q , R , T ৶ড়а§Ца§Ња§П а§Ча§П а§єа•Иа•§ `PQ = QR = RT = (vt _(0 ))/(3 )` а§≤а§ња§ѓа§Њ а§Ча§ѓа§Њ а§єа•Иа•§
ুৌ৮ а§≤а•За§В а§Ха•З t = 0 ৙а§∞ ১а§∞а§Ва§Ча§Ња§Ча•На§∞ `Sigma _(1 )` а§Ха•З а§ђа§Ња§Па§Б а§Хড়৮ৌа§∞а•З, а§Еа§∞а•Н৕ৌ১ P а§ђа§ња§В৶а•Б ৙а§∞ ৙৺а•Ба§Ба§Ъ১ৌ а§єа•Иа•§ а§За§Єа•А а§Єа§Ѓа§ѓ а§ѓа§єа§Ња§Б а§Єа•З а§Па§Х а§Ча•Ла§≤а§Ња§Ха§Ња§∞ ৶а•Н৵ড়১а•Аа§ѓа§Х ১а§∞а§Ва§Ча§ња§Ха§Њ ( secondary wavelet ) а§Ъа§≤৮ৌ ৙а•На§∞а§Ња§∞а§Ѓа•На§≠ а§Ха§∞а•За§Ча•А а•§ `t = t _(0 )` ৙а§∞ а§За§Є ১а§∞а§Ва§Ча§ња§Ха§Њ (wavelet ) а§Ха•А ১а•На§∞а§ња§Ьа•На§ѓа§Њ `vt _(0 )` а§єа•Л а§Ьа§Ња§Па§Ча•А а•§ а§Ъড়১а•На§∞ а§Ѓа•За§В а§ѓа§є ১а§∞а§Ва§Ча§ња§Ха§Њ `W _(1 )` а§єа•И а§Ьа§ња§Єа§Ха•А ১а•На§∞а§ња§Ьа•На§ѓа§Њ PT а§Ха•З а§ђа§∞а§Ња§ђа§∞ а§єа•Иа•§
а§Ѓа•Ва§≤ ১а§∞а§Ва§Ча§Ња§Ча•На§∞ AB а§ђа§ња§В৶а•Б Q ৙а§∞ `t = (t _(0 ))/(3 )` а§Єа§Ѓа§ѓ ৙а§∞ ৙৺а•Ба§Ба§Ъа•За§Ча§Ња•§ а§За§Є а§Єа§Ѓа§ѓ ৙а§∞ а§ѓа§є а§ђа§ња§В৶а•Б ৶а•Н৵ড়১а•Аа§ѓа§Х ১а§∞а§Ва§Ча§ња§Ха§Њ а§Й১а•Н৙৮а•Н৮ а§Ха§∞৮ৌ ৙а•На§∞а§Ња§∞а§Ѓа•На§≠ а§Ха§∞а•За§Ча§Ња•§ `t = t _(0 )` ৙а§∞ а§За§Є ১а§∞а§Ва§Ча§ња§Ха§Њ а§Ха•Л а§Й১а•Н৙৮а•Н৮ а§єа•Ба§П `(2t _(0 ))/(3 )` а§Єа§Ѓа§ѓ а§ђа•А১ а§Ъа•Ба§Ха§Њ а§єа•Ла§Ча§Њ ১৕ৌ а§За§Єа§Ха•А ১а•На§∞а§ња§Ьа•На§ѓа§Њ `(2vt _(0 ))/(3 ) ` а§єа•Л а§Ьа§Ња§Па§Ча•Аа•§ а§ѓа§є ১а§∞а§Ва§Ча§ња§Ха§Њ а§Ъড়১а•На§∞ а§Ѓа•За§В `W _(2 )` а§Єа•З ৶ড়а§Ца§Ња§И а§Ча§И а§єа•Иа•§ а§За§Єа§Ха•А ১а•На§∞а§ња§Ьа•На§ѓа§Њ QT а§Ха•З а§ђа§∞а§Ња§ђа§∞ а§єа•Иа•§
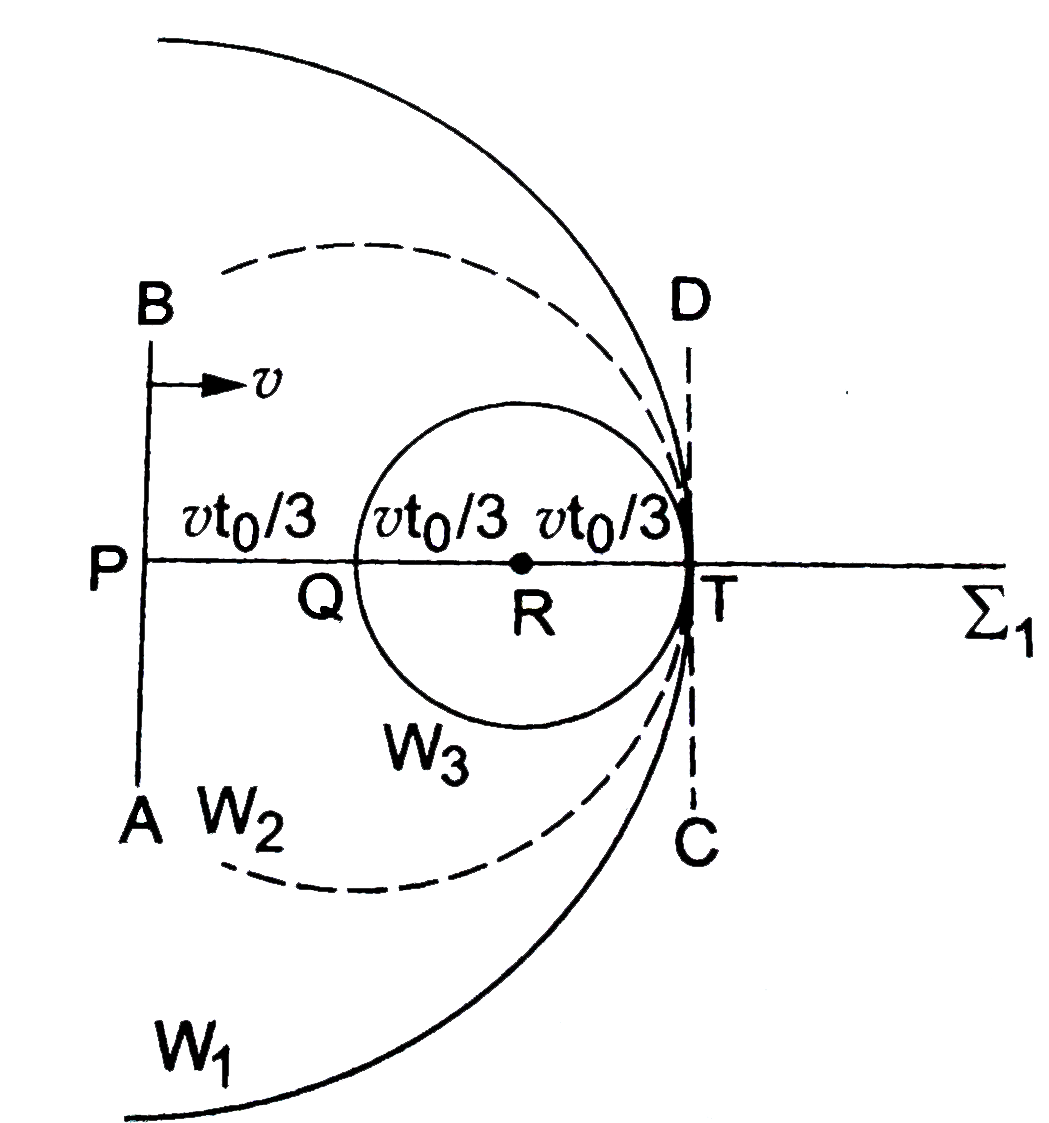
১а§∞а§Ва§Ча§Ња§Ча•На§∞ AB а§ђа§ња§В৶а•Б R ৙а§∞ `t _(0 )=(2t _(0 ))/(3 )` ৙а§∞ ৙৺а•Ба§Ба§Ъа•За§Ча§Ња•§ а§За§Є а§Єа§Ѓа§ѓ а§ѓа§є ৶а•Н৵ড়১а•Аа§ѓа§Х ১а§∞а§Ва§Ча§ња§Ха§Њ а§Й১а•Н৙৮а•Н৮ а§Ха§∞৮ৌ ৙а•На§∞а§Ња§∞а§Ѓа•На§≠ а§Ха§∞а•За§Ча§Ња•§ `t = t _(0 )` ৙а§∞ а§За§Є ১а§∞а§Ва§Ча§ња§Ха§Њ а§Ха•Л а§Й১а•Н৙৮а•Н৮ а§єа•Ба§П `(t _(0 ))/(3 )` а§єа•Л а§Ъа•Ба§Ха•А а§єа•Ла§Ча•Аа•§ а§Ъড়১а•На§∞ а§Ѓа•За§В а§ѓа§є ১а§∞а§Ва§Ча§ња§Ха§Њ `W _(3 )` а§Єа•З ৶ড়а§Ца§Ња§И а§Ча§И а§єа•И ১৕ৌ а§За§Єа§Ха•А ১а•На§∞а§ња§Ьа•На§ѓа§Њ RT а§Ха•З а§ђа§∞а§Ња§ђа§∞ а§єа•И а§За§Єа•А ৙а•На§∞а§Ха§Ња§∞ а§Ж৙ `Sigma _(1 )` а§Ха•З а§Ха§ња§Єа•А а§≠а•А а§ђа§ња§В৶а•Б а§Єа•З а§Й১а•Н৙৮а•Н৮ ১а§∞а§Ва§Ча§ња§Ха§Њ а§Ха•Л `t = t _(0 )` а§Єа§Ѓа§ѓ ৙а§∞ а§Ца•Аа§Ва§Ъа•З ১а•Л ৵৺ T а§ђа§ња§В৶а•Б а§Єа•З а§Ча•Ба§Ьа§∞а•За§Ча•Аа•§ а§З৮ а§Єа§≠а•А а§Ча•Ла§≤а§Ња§Ха§Ња§∞ ৪১৺а•Ла§В ৙а§∞ а§Жа§Ча•З а§Ха•А ৶ড়৴ৌ а§Ѓа•За§В а§Па§Х а§Єа•Н৙а§∞а•Н৴ ৪১৺ а§Ца•Аа§Ва§Ъа•За§Ча•З ১а•Л ৵৺ CD а§єа•Ла§Ча•Аа•§ а§ѓа§єа•А CD ৪১৺ `t = t _(0 )` ৙а§∞ AB ১а§∞а§Ва§Ча§Ња§Ча•На§∞ а§Ха§Њ ৮ৃৌ а§Єа•Н৕ৌ৮ а§єа•Иа•§