x² + y² - 4x -6y - 12 = 0 and x² + y² + 6x + 18y + 26 = 0 What is the number of common tangents to circles?

Question

x² + y² - 4x -6y - 12 = 0 and x² + y² + 6x + 18y + 26 = 0 What is the number of common tangents to circles?

Answer 1

 x² +y² +6x+18x+26=0 

⇒x² +2.3x+9+y² +2.9x+81b=81+9−26 

=(x+3) 2 +(y+9)² =8² 

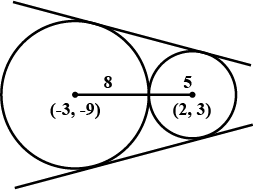
Center (−3,−9),radius=8 

x² +y² −4x−6y−12=0 

⇒x² −2.2x+4+y 2 −2.3y+9=12+9+4 

⇒(x−2)² +(y−3)² =5² 

Center (2,3),radius=5 

distance between centers 

\(\sqrt{(2+3)^2 +(3+9)^2} \)​ =13=8+5 Sum of radius. 

we know that if the distance between circles is equal to sum of radius of the circles then they are only 2 common tangents 

∴ only 2 common tangents possible