Correct option is: (B) rhombus
A parallelogram circumscribing a circle is a rhombus.
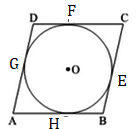
\(\because\) Tangents are of equal length from a fixed outer point to circle.
\(\therefore\) AH = AG ....(1) (Tangents to circle from point A).
BH = BE ....(2) (Tangents to circle from point B).
CF = CE ....(3) (Tangents to circle from point C).
DF = DG ....(4) (Tangents to circle from point D).
By adding equations (1), (2), (3) & (4), we get.
AH + BH + CF + DF = AG + BE + CE + DG.
= (AH + BH) + (CF + DF) = (AG + DG) + (BE + CE).
= AB + CD = AD + BC.
= 2 AB = 2 BC (\(\because\) AD = BC & CD = AB as opposite sides in a parallelogram are equal).
= AB = BC.
\(\therefore\) CD = AB = BC = AD.
\(\therefore\) Parallelogram ABCD is rhombus.