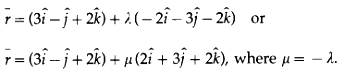The line \(\bar{r} = (\hat{i} + \hat{j} - \hat{k}) + \lambda (2\hat{i} - 2\hat{j} + \hat{k})\) is parallel to the vector \(\bar{b} = 2\hat{i} - 2\hat{j} + \hat{k}\) and the line \(\bar{r} = (2\hat{i} + \hat{j} - 3\hat{k}) + \mu (\hat{i} - 2\hat{j} + 2\hat{k})\) is parallel to the vector \(\bar{c} = \hat{i} - 2\hat{j} + 2\hat{k}.\)
The vector perpendicular to the vectors \(\bar{b}\) and \(\bar{c}\) is given by

Since the required line is perpendicular to the given lines, it is perpendicular to both \(\bar{b}\) and \(\bar{c}\).
∴ it is parallel to \(\bar{b}\) × \(\bar{c}\)
The equation of the line passing through A(\(\bar{a}\)) and parallel to \(\bar{b}\) × \(\bar{c}\) is

∴ the equation of the required line is