Given equation is x2 + 3ix + 10 = 0
Comparing with ax2 + bx + c = 0, we get
a = 1, b = 3i, c = 10
Discriminant = b2 – 4ac
= (3i)2 – 4 × 1 × 10
= 9i2 – 40
= -9 – 40 ……[∵ i2 = -1]
= -49 < 0
So, the given equation has complex roots.
These roots are given by
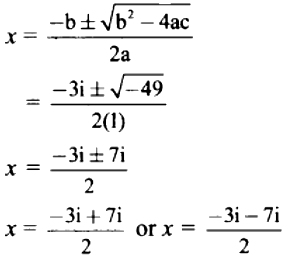
∴ x = 2i or x = -5i
∴ The roots of the given equation are 2i and -5i.