Question

In a parallelogram, if one set of opposite angles are complementary, then the biggest angle in it is

A) 270° 

B) 45° 

C) 90° 

D) 135°

Answer 1

Correct option is (D) 135°

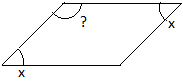
Let one of opposite angle is x.

\(\therefore\) x+x = \(90^\circ\)   \((\because\)  Opposite angles are equal in parallelogram)

\(\Rightarrow\) 2x = \(90^\circ\)

\(\Rightarrow\) x = \(\frac{90^\circ}2=45^\circ\)

\(\therefore\) It's consecutive angle \(=180^\circ-x\)

\(=180^\circ-45^\circ=135^\circ\)

Then biggest angle is \(135^\circ.\)

Answer 2

Correct option is  D) 135°