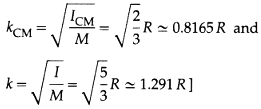Question

State the expression for the MI of a thin spherical shell (i.e., a thin-walled hollow sphere) about its diameter. Hence obtain the expression for its MI about a tangent.

Answer 1

Consider a uniform, thin-walled hollow sphere radius R and mass M. An axis along its diameter is an axis of spherical symmetry through its centre of mass. The MI of the thin spherical shell about its diameter is I_CM = \(\frac23\) MR²

Let I be its MI about a tangent parallel to the diameter. Here, h = R = distance between the two axes. Then, according to the theorem of parallel axis,