Question

A steel ball floats in a vessel with mercury.

How will the volume of the part of the ball submerged in mercury change if a layer of water completely covering the ball is poured above the mercury?

Answer 1

Let the volume of the steel ball be V, and let the volume of its part immersed in mercury be V₀ before water is poured and V₁ after water covers the ball completely. The value of V₀ can be found from the condition

where ρ_st and ρ_mer are the densities of steel and mercury. Since the pressure of water is transmitted through mercury to the lower part of the ball, the buoyant force exerted on it by water is ρ_w (V - V₁) g, where p, is the density of water, while the buoyancy of mercury is ρ_mer V₁g. The condition of floating for the ball now becomes 

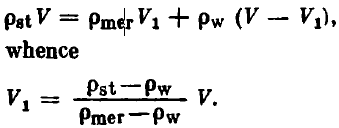
Thus, the ratio of the volumes of the parts of the ball submerged in mercury in the former and latter cases is

i.e. the volume of the part of the ball immersed in mercury will become smaller when water is poured.