Let us analyze the operation of the heat engine based on the cycle formed by two isotherms and two isochors (Fig. 200).
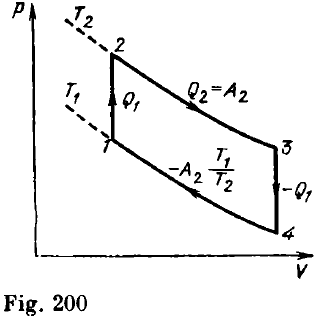
Suppose that the temperature of the cooler (corresponding to the lower isotherm) is T1, and the temperature of the heater (corresponding to the upper isotherm) is T2. On the isochoric segment 1-2, the gas volume does not change, i.e. no work is done, but the temperature increases from T1 to T2. It means that a certain amount of heat Q1 is supplied to the gas. On the isothermal segment 2-3, the internal energy of the gas remains constant, and the entire amount of heat Q2 supplied to the gas is spent on doing work: Q2 = A2.
On the isochoric segment, 3-4, the gas temperature returns to its initial value T1, i.e. the amount of heat Q1 is removed from the gas. On the isothermal segment 4-1, the work done by the gas is negative, which means that some amount of heat is taken away from the gas. Thus, the total amount of heat supplied to the gas per cycle is Q1 + A2. Figure 200 shows that the work done by the gas per cycle is the sum of the positive work A2 on the segment 2-3 and the negative work A4 on the segment 4-1.
Let us compare the pressures at the points corresponding to equal volumes on the segments 4-1 and 2-3. The Gay-Lussac law indicates that the ratio of these pressures is T1/T2, and hence the work done by the gas is A4 = (T1/T2) A2. The total work per cycle is given by
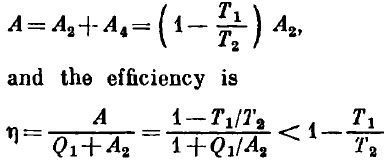
Therefore, the efficiency of the heat engine based on the cycle consisting of two isotherms and two isochors is lower than the efficiency 1 - T1/T2 of Carnot's heat engine.