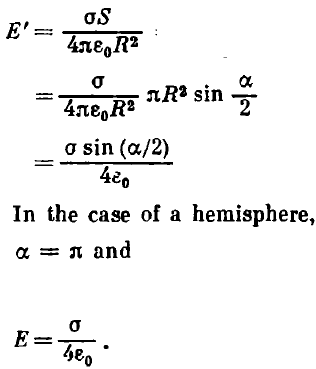If a charge is distributed with a constant density σ over a part of the spherical surface of radius R, the projection of the electric field strength due to this charge at the centre of the spherical surface on an arbitrary direction a is
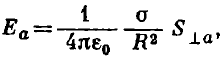
where S⊥a is the area of the projection of the part of the surface on the plane perpendicular to the direction a.
Let us consider a certain region of the spherical surface ("lobule") and orient it as shown in Fig. 207, i.e. make the symmetry plane of the lobule coincide with the z- and x-axes. From the symmetry of charge distribution it follows that the total field strength at the origin of the coordinate system (point O) will be directed against the z-axis (if σ > 0), and the field strength components along the x- and y-axes will be zero
Let us consider a small region of the surface ΔS of the lobule. The vertical component of the electric field strength at point O produced by the surface element ΔS is given by
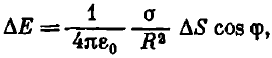
where φ is the angle between the normal to the area element and the vertical. But ΔS cos φ is the
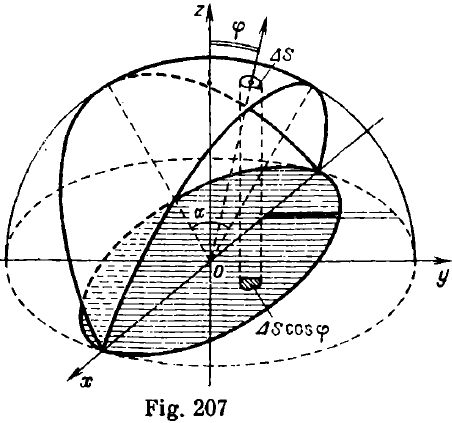
area of the projection of the element ΔS on the horizontal plane. Hence the total field strength at point O can be determined from the formula
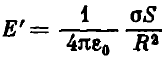
where S is the area of the hatched figure in Fig. 207, which is the projection of the lobule on the horizontal plane xOy. Since the area of any narrow strip of this region (black region in Fig. 207) is smaller than the area of the corresponding strip of the large circle by a factor of sin (α/2), the entire area of the hatched region is smaller than the area of the large circle by a factor of sin (α/2). Hence