Question

Prove that the locus of the poles of chords which are normal to the parabola y² = 4ax is the curve y²(x + 2a) + 4a³ = 0.

Answer 1

Let PQ be a chord which is normal at P. Its equation is then

y = mx - 2am - am³ .......(1)

Let the tangents at P and Q. intersect in T, whose coordinates are h and k, so that we require the locus of T.

Since PQ is the polar of the point {h, k) its equation is

yk = 2a(x + h) ....(2)

Now the equations (1) and (2) represent the same straight line, so that they must be equivalent. Hence

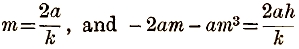
Eliminating m, i.e. substituting the value of m from the first of these equations in the second, we have

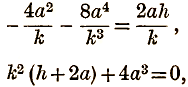
The locus of the point T is therefore

y²(x + 2a) + 4a³ = 0.