First, we draw the lines
3x + 3y = 18 ...(1)
and 3x + 2y = 15 ...(2)
The shaded region OCPB is the feasible region.
The vertices of the feasible region are C (5, 0), P (3, 3), B (0, 6) and O (0, 0)
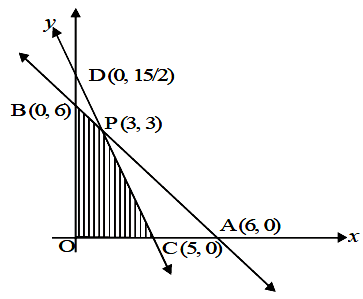
By solving (1) & (2) we get co-ordinate of corner.
The value of z = 30x + 25y at the corner points are as :
z = 30x + 25y
At O (0, 0), Z = 30 × 0 + 25 × 0 = 0
At P (3, 3), Z = 30 × 3 + 25 × 3 = 90 + 75 = 165
At C (5, 0) Z = 30 × 5 + 25 × 0 = 150
At B (0, 6), Z = 30 × 0 + 25 × 6 = 150
Clearly maximum Z is 165 at (3, 3) i.e. when x = 3 and y = 3