Question

Prove that cot² π/6 + cosec 5π/6 + 3 tan² π/6 = 6.

Answer 1

Taking L.H.S.

Cos² \(\cfrac{\pi}6\) + cosec \(\cfrac{5\pi}6\) + 3 tan² \(\cfrac{\pi}6\)

Putting \(\pi\) = 180\(^\circ\)

Here, 

tan 30\(^\circ\) = \(\cfrac{1}{\sqrt3}\)

cot  30\(^\circ\) = \(\cfrac{1}{tan \,30^\circ}\) 

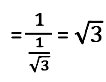
For cosec 150\(^\circ\),

First, Finding sin  150\(^\circ\)

sin  150\(^\circ\) = sin (180 - 30\(^\circ\))

= sin 30\(^\circ\) = \(\cfrac{1}2\)

cosec 150\(^\circ\) = \(\cfrac{1}{sin \,150^\circ}\)

= \(\cfrac{1}{\cfrac{1}{2}}\) = 2

Putting values 

= cot² 30\(^\circ\) + cosec (150\(^\circ\)) + 3tan² 30\(^\circ\)

= 3 + 2 + 3 x \(\cfrac13 \)

= 3 + 2 + 1

= 6

= R.H.S

Hence proved