Question

Without performing division, state whether the following rational numbers will have a terminating decimal form or a non-terminating, repeating decimal form.

i) \(\frac{23}{2^3.5^2}\)

ii) \(\frac{129}{2^2.5^7.7^5}\)

iii) \(\frac{9}{15}\)

iv) \(\frac{36}{100}\)

v) \(\frac{77}{210}\)

Answer 1

i) \(\frac{23}{2^3.5^2}\)

\(\frac{23}{2^3.5^2}\) is a terminating decimal. 

[∵ The denominator is of the form 2ⁿ. 5^m]

ii) \(\frac{129}{2^2.5^7.7^5}\)

\(\frac{129}{2^2.5^7.7^5}\)is a non terminating, repeating decimal.

iii) \(\frac{9}{15}\)

\(\frac{9}{15}\) = \(\frac{3}{5}\)

Denominator is of the form 2ⁿ. 5^m. 

∴\(\frac{9}{15}\) = \(\frac{3}{5}\) is a terminating decimal.

iv) \(\frac{36}{100}\)

100 = 2² × 5² is of the form 2ⁿ . 5^m 

Hence \(\frac{36}{100}\) is a terminating decimal.

v) \(\frac{77}{210}\)

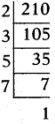
210 = 2 × 3 × 5 × 7 is not of the form 2ⁿ. 5^m

Given fraction has a non-terminating, repeating decimal expansion.