Question

A solid is in the form of a right circular cylinder with a hemisphere at one end and a cone at the other end. The radius of the common base is 8 cm and the heights of the cylindrical and conical portions are 10 cm and 6 cm respectively. Find the total surface area of the solid.

Answer 1

Total surface area = C.S.A. of the cone + C.S.A. of cylinder + C.S.A of the hemisphere.

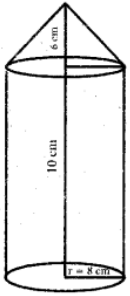
Cone: 

Radius (r) = 8 cm 

Height (h) = 6 cm 

Slant height l = \(\sqrt{r^2+h^2}\)

= \(\sqrt{8^2+6^2}\)

= \(\sqrt{64+36}\)

= √100 

= 10 cm 

C.S.A. = πrl 

= 22/7 × 8 × 10 

= \(\frac{1760}{7}\) cm²

Cylinder: 

Radius (r) = 8 cm; 

Height (h) = 10 cm 

C.S.A. = 2πrh 

= 2 × \(\frac{22}{7}\) × 8 × 10 

= \(\frac{3520}{7}\) cm² 

Hemisphere: 

Radius (r) = 8 cm 

C.S.A. = 2πr² 

= 2 × \(\frac{22}{7}\) × 8 × 8 

= \(\frac{2816}{7}\) cm² 

∴ Total surface area of the given solid 

= \(\frac{1760}{7}\) + \(\frac{3520}{7}\) + \(\frac{2816}{7}\)

T.S.A. = \(\frac{8096}{7}\) = 1156.57 cm².