84. Show that the right circular cylinder of given surface and maximum volume is such that is heights is equal to the diameter of the base.
Answer:
Let r and h be the radius and height of the cylinder respectively.
Then, the surface area (S) of the cylinder is given by,

Let V be the volume of the cylinder. Then,

∴ By second derivative test, the volume is the maximum when \(r^2 = \frac S{6\pi}\)
Now, when \(r^2 = \frac S{6\pi}\), then \(h = \frac{6\pi r^2}{2\pi}\left(\frac1r\right)-r = 3r - r = 2r\).
Hence, the volume is the maximum when the height is twice the radius i.e., when the height is equal to the diameter.
85. Of all the closed cylindrical cans (right circular), of a given volume of 100 cubic centimeters, find the dimensions of the can which has the minimum surface area?
Answer:
Let r and h be the radius and height of the cylinder respectively.
Then, volume (V) of the cylinder is given by,
\(V = \pi r^2h = 100\) (given)
\(\therefore h = \frac{100}{\pi r^2}\)
Surface area (S) of the cylinder is given by,

Now, it is observed that when \(r = \left(\frac{50}{\pi}\right)^{\frac13},\frac{d^2S}{dr^2}> 0.\)
∴ By second derivative test, the surface area is the minimum when the radius of the cylinder is \(\left(\frac{50}{\pi}\right)^{\frac13}\)
When \(r =\left(\frac{50}{\pi}\right)^{\frac13}\)
\(h = \frac{100}{\pi\left(\frac{50}\pi\right)^{\frac23}} = \frac{2\times 50}{(50)^{\frac23}(\pi)^{1 - \frac23}} = 2 \left(\frac{50}{\pi}\right)^{\frac13} cm\)
Hence, the required dimensions of the can which has the minimum surface area is given by radius = \(\left(\frac{50}{\pi}\right)^{\frac13}cm\) and height = \(2\left(\frac{50}{\pi}\right)^{\frac13}cm\).
86. A wire of length 28 m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a circle. What should be the length of the two pieces so that the combined area of the square and the circle is minimum?
Answer:
Let a piece of length l be cut from the given wire to make a square.
Then, the other piece of wire to be made into a circle is of length (28 − l) m.
Now, side of square = \(\frac l4\)
Let r be the radius of the circle.
Then,
\(2\pi r = 28 - 1 \)
⇒ \(r = \frac1{2\pi }(28 -l)\)
The combined areas of the square and the circle (A) is given by,

Thus, when \(l = \frac{112}{\pi + 4}, \frac{d^2A}{dl^2}>0.\)
\(\therefore\) By second derivative test, the area (A) is the minimum when \(l = \frac{112}{\pi + 4}\).
Hence, the combined area is the minimum when the length of the wire in making the square is \( \frac{112}{\pi + 4}\) cm while the length of the wire in making the circle is \(28 - \frac{112}{\pi + 4} cm.\)
87. Prove that the volume of the largest cone that can be inscribed in a sphere of radius R is 8/27 of the volume of the sphere.
Answer:
Let r and h be the radius and height of the cone respectively inscribed in a sphere of radius R.
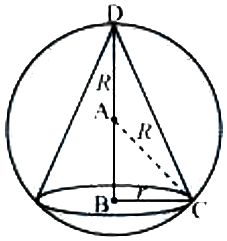
Let V be the volume of the cone.
Then,
\(V = \frac13 \pi r^2h\)
Height of the cone is given by,
h = R + AB
\(= R + \sqrt{R^2 - r^2}\) [ABC is a right triangle]

∴ By second derivative test, the volume of the cone is the maximum when \(r^2 = \frac89 R^2.\)

Hence, the volume of the largest cone that can be inscribed in the sphere is \(\frac8{27}\) the volume of the sphere.
88. Show that the right circular cone of least curved surface and given volume has an altitude equal to √2 time the radius of the base.
Answer:
Let r and h be the radius and the height (altitude) of the cone respectively.
Then, the volume (V) of the cone is given as:
\(V = \frac1{3\pi}\pi r^2 h\)
⇒ \(h = \frac {3V}{r^2}\)
The surface area (S) of the cone is given by,
S = πrl (where l is the slant height)


Thus, it can be easily verified that when \(r^6 = \frac{9V^2}{2\pi ^2} , \frac{d^2S}{dr^2}>0. \)
∴ By second derivative test, the surface area of the cone is the least when \(r^6 = \frac{9V^2}{2\pi^2}.\)

Hence, for a given volume, the right circular cone of the least curved surface has an altitude equal to √2 times the radius of the base.
89. Show that the semi-vertical angle of the cone of the maximum volume and of given slant height is tan-1 √2.
Answer:
Let θ be the semi-vertical angle of the cone.
It is clear that \(\theta \in\left[0, \frac{\pi}{2}\right].\)
Let r, h, and l be the radius, height, and the slant height of the cone respectively.
The slant height of the cone is given as constant.

Now, r = l sin θ and h = l cos θ
The volume (V) of the cone is given by,

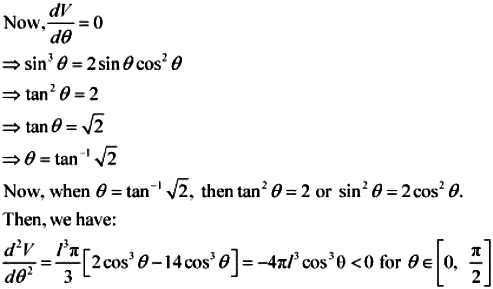
By second derivative test, the volume (V) is the maximum when \(\theta = tan^{-1}\sqrt2\)
Hence, for a given slant height, the semi-vertical angle of the cone of the maximum volume is \( tan^{-1}\sqrt2.\)