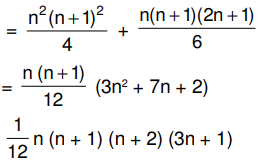Question

Find the nth term and the sum of n term of the series 2, 12, 36, 80, 150, 252.

Answer 1

Let S = 2 + 12 + 36 + 80 + 150 + 252 + ................+T_n ...........(i) 

S = 2 + 12 + 36 + 80 + 150 + 252 + .........+T_n–1 + T_n ...........(ii) 

(i) – (ii) ⇒ T_n = 2 + 10 + 24 + 44 + 70 + 102 + ............... + (T_n – T_n–1) ...........(iii) 

T_n = 2 + 10 + 24 + 44 + 70 + 102 + ....... + (T_n–1–T_n–2) + (T_n – T_n–1) ...........(iv) 

(iii) – (iv) ⇒ T_n – T_n–1 = 2 + 8 + 14 + 20 + 26 + ......... 

= n/2[4 + (n – 1) 6] = n [3n – 1] = T_n – T_n–1 = 3n² – n

∴ general term of given series is ∑ T_n – T_n–1 = ∑ 3n² – n = n³ + n². 

Hence sum of this series is S = ∑ n³ + ∑ n²