Question

For the straight lines 4x + 3y – 6 = 0 and 5x + 12y + 9 = 0, find the equation of the 

(i) bisector of the obtuse angle between them; 

(ii) bisector of the acute angle between them;

Answer 1

(i) The equations of the given straight lines are 

4x + 3y – 6 = 0 ........(1) 

5x + 12y + 9 = 0 ........(2) 

The equation of the bisectors of the angles between lines (1) and (2) are

or 52x + 39y – 78 = 25x + 60y + 45 

or 27x – 21y – 123 = 0 or 9x – 7y – 41 = 0 

Taking the negative sign, we have

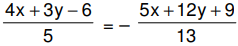
or 52x + 39y – 78 = –25x – 60y – 45 

or 77x + 99y – 33 = 0 or 7x + 9y – 3 = 0 

Hence the equation of the bisectors are 

9x – 7y – 41 = 0 ........(3) 

and 7x + 9y – 3 = 0 ........(4)

Now slope of line (1) = - 4/3 

and slope of the bisector (3) = 9/7.

If θ be the acute angle between the line (1) and the bisector (3), then

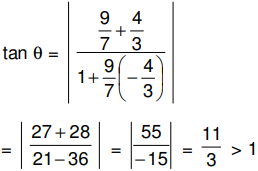
∴ θ > 45º 

Hence 9x – 7y – 41 = 0 is the bisector of the obtuse angle between the given lines (1) and (2) 

(ii) Since 9x – 7y – 41 is the bisector of the obtuse angle between the given lines, therefore the other bisector 7x + 9y – 3 = 0 will be the bisector of the acute angle between the given lines.

2nd Method : 

Writing the equation of the lines so that constants become positive we have 

– 4x – 3y + 6 = 0 .......(1) 

and 5x + 12y + 9 = 0 .......(2) 

Here a₁ = – 4, a₂ = 5, b₁ = –3, b₂ = 12 

Now a₁ a₂ + b₁ b₂ = – 20 – 36 = –56 < 0 

∴ origin does not lie in the obtuse angle between lines (1) and (2) and hence equation of the bisector of the obtuse angle between lines (1) and (2) will be

or 13(–4x – 3y + 6) = –5(5x + 12y + 9) 

or 27x – 21y – 123 = 0 

or 9x – 7y – 41 = 0 

 and the equation of the bisector of the acute angle will be (origin lies in the acute angle)

or 77x + 99y – 33 = 0 

or 7x + 9y – 3 = 0