Given circle is x2 + y2 – 6x + 4y – 12 = 0 .......(i)
and given line is 4x + 3y + 5 = 0 .......(ii)
Centre of circle (i) is (3, –2) and its radius is 5.
Equation of any line
4x + 3y + k = 0 parallel to the line (ii) .......(iii)
If line (iii) is tangent to circle, (i) then
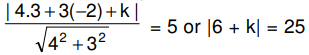
or 6 + k = ± 25
∴ k = 19, – 31
Hence equation of required tangents are 4x + 3y + 19 = 0 and 4x + 3y – 31 = 0