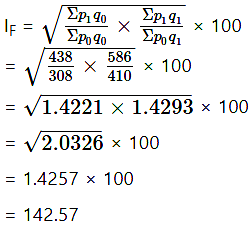Here,
p0 = Price in 2014
q0 = Quantity in 2014,
P1 = Price in 2015,
q1 = Quantity in 2015.
After making the units of price and quantity, we will compute the ideal index number, i.e., Fisher’s index number.
Explanation :
Item A: The unit of price is 20 kg and the unit of quantity is kg.
∴ In 2014. the price per kg = \(\frac{120}{20}\) = ₹ 6
In 2015, the price per kg = \(\frac{280}{20}\) = ₹ 14
Item B: The unit of price is 5 dozen and the unit of quantity is dozen.
∴ In 2014, the price per dozen = \(\frac{120}{5}\) = ₹ 24
In 2015, the price per dozen = \(\frac{140}{5}\) = ₹ 28
In 2015, the quantity in dozen = \(\frac{48}{12}\) = 4 dozen
Item C : The unit of price is kg and the unit of quantity is gram.
∴ In 2014, the quantity in kg = \(\frac{5000}{1000}\) = 5 kg
Item D : The unit of price is 5 litre and the unit of quantity is litre.
∴ In 2014, the price per litre = \(\frac{52}{5}\)= ₹ 10.40
In 2015. the price per litre = \(\frac{58}{5}\) = ₹ 11.60
To compute Fisher’s index number, the table for calculation is prepared as follows:
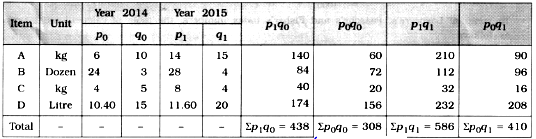
Fisher’s index number: