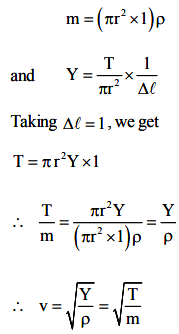When a string, having a linear mass density m (i.e. m = mass per unit length of the string), is stretched by a tension T, the speed of propagation of waves, through it, is given by
\(v=\sqrt{\frac{T}{m}}\)
Remembering that the relevant modulus of elasticity, for a string, is the Young’s modulus of its material, it is easy to see that this formula is consistent with the formula
\(v=\sqrt{\frac{Y}{ρ}}\)
This is so because