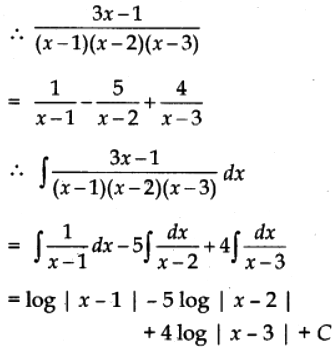Evaluate : ∫ 3x-1/(x-1)(x-2)(x-3) dx.

Question

Evaluate : ∫ \(\frac{3x-1}{(x-1) (x-2) (x-3)}\) dx.

Answer 1

Let

⇒ 3x – 1 = A(x – 2)(x – 3) + B(x – 1)(x – 3) + C(x – 1)(x – 2)

⇒ 3x – 1 = A(x² – 5x + 6) + B(x² – 4x + 3) + C(x² – 3x + 2)

⇒ 3x – 1 = (A + B + Cx² + (- 5A – 4B – 3C)x + 6A + 3B + 2 C

Comparing the coeffcients of x², x and constant terms in both sides, we have

A + B + C = 0

– 5A – 4B – 3C = 3

and 6A + 3B + 2C = -1

Now, solving these equations, we get

A = 1, B = -5, C = 4