Question

Two electrons move in a central field. Consider the electrostatic interaction e²/|r₁ - r₂| between the electrons as a perturbation.

(a) Find the first order energy shifts for the states (terms) of the (1s)(2s) configuration. (Express your answers in terms of unperturbed quantities and matrix elements of the interaction e²/(|r₁ - r₂|)

(b) Discuss the symmetry of the two-particle wave function for the states in part (a).

(c) Suppose that, at time t = 0, one electron is found to be in the 1s unperturbed state with spin up and the other electron in the 2s unperturbed state with spin down as shown in Fig. At what time t will the occupation of the states be reversed?

Answer 1

(a) The zero order wave function of the two electrons has the forms

being the normalized symmetric (+) and antisymmetric (-) wave functions, x₀ and x₁ denote the singlet and triplet spin states respectively. Denoting \(u_{1s}(1)v_{2s}(2) \) by \(|1,2\rangle\) and \(u_{1s}(2)v_{2s}(1)\) by \(|2,1\rangle\), we can write the above as

Because the perturbation Hamiltonian is independent of spin, we need not consider x. Thus

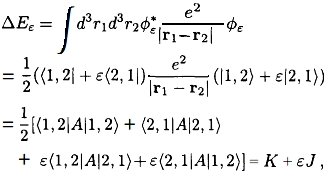
where \(A =e^2|r_1 - r_2|, K = \langle 1,2|A|1,2\rangle = \langle 2,1|A|2,1\rangle\)is the direct integral, \(J = \langle 1,2|A|2,1\rangle = \langle 2, 1|A| 1,2\rangle \) is the exchange integral.

(b) The singlet state x₀ is antisymmetric for interchange of spins. The triplet state x₁ is symmetric for interchange of spins. Similarly, \(\phi_+\) is symmetric for the interchange of r₁ and r₂, and \(\phi_-\) is antisymmetric for the interchange. Hence the total wave function is always antisymmetric for interchange of the electrons.

(c) The initial state of the system is

which shows that at this time the 1s electron has spin down and the 2s electron has spin up i.e., the spins are reversed. As -1 = e^i(2n+1)π, n = 0,1, 2..., this happens at times