Question

Describe the low-lying states of the H₂ molecule. Give a rough value for their excitation energies. Characterize the radiative transitions of the first two excited states to the ground state.

Answer 1

In an approximate treatment of hydrogen atom, the zero order wave function is taken to be the product of two ground state hydrogen-like wave functions, which have the form

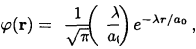
where a₀ is the Bohr radius, \(\lambda\) is a parameter to be determined. The spin part of the electron wave function of the Hz molecule ground state (S = 0) is antisymmetric which requires the spatial part to be symmetric. As the spins of the two electrons are antiparallel, they can get quite close to each other (Pauli's principle). This means that the density of "electron cloud” is rather large in the region of space between the two nuclei. In this region, the attractive potential between the two electrons and the two nuclei is quite large and thus can form a bound state, with wave function

where the variables are as shown in Fig.

If the spins of the electrons are parallel (S = 1), then the spatial wave function must be antisymmetric, the probability that the two electrons getting close is small, and no bound state occurs.

Of the energy levels related to the electronic, vibrational and rotational motions of H₂, the rotational levels have the smallest spacing between two adjacent levels. For simplicity, we shall only consider rotational energy levels with the electrons in the ground state initially and in the absence of vibration between the nuclei. With no loss of generality, we can take the molecule's energy to be zero when there is no rotation. The rotational levels are given by

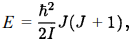
where I is the moment of inertia and J is the total angular momentum of the two-nuclei system. When J = even, the total spin of the two protons in H₂ is S = 0 and para-hydrogen results; when J = odd, the total spin of the two protons is S = 1 and ortho-hydrogen results. Suppose the distance between the two protons is R = 1.5 x 0.53 = 0.80 Å (Fig.). As

As the interactions between two atoms are spin-independent, para-hydrogen and ortho-hydrogen cannot transform to each other, hence the selection rule AJ = even. In nature the ratio of the number of molecules of ortho-hydrogen to that of para-hydrogen is 3:1. This means that the spectral line for J = 2 → J = 0 is weaker than for J = 3 → J = 1.