Question

A function f : R - {-1, 1} -> R is defined by:

\(f(X)=\frac{x}{x^2-1}\)

i) Check if f is one-one. 

ii) Check if f is onto.

Answer 1

i) Assumes f(x) = f(y) and evaluates the same as:

Uses the above step to conclude that x = y or xy = -1.

Takes a pair of numbers x and y such that xy = -1 to show that f is not one-one.

For example,

for x = 1/2 and y = -2, f(x) = − 2/3 and f(y) = − 2/3 .

ii) Equates f(x) to y and solves the same to express x in terms of y as:

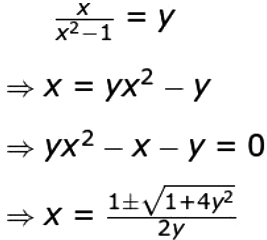
Since 1 + 4y² > 0, real root exists and also they are not ± 1

⇒ \(x=\frac{1\pm \sqrt {1+4y^2}}{2y} \in R-\{-1,+1\}\)

Writes that for any y ∈ R (codomain), there exists x ∈ R - {-1, 1} (domain) such that f(x) = y. Hence concludes that f is onto.