In △ABC, DE || BC (as shown in the figure). If AD = 2 cm, BD = 3 cm, BC = 7.5 cm, then the length of DE (in cm) is:

Question

In \(\triangle ABC\), DE || BC (as shown in the figure). If AD = 2 cm, BD = 3 cm, BC = 7.5 cm, then the length of DE (in cm) is:

(A) 2.5

(B) 3

(C) 5

(D) 6

Answer 1

Correct option is (B) 3

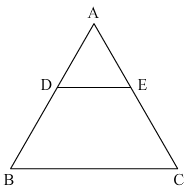
In \(\triangle ABC\), D and E are points on the sides AB and AC, respectively such that DE || BC.

In \(\triangle ADE\) and \(\triangle ABC\),

\(\angle DAE = \angle BAE\) (Common)

\(\angle AED = \angle ACB\) (Corresponding angles)

\(\therefore\) \(\triangle ADE \sim\triangle ABC\) (AA Similarity)

\(\Rightarrow\frac{DE}{BC} = \frac{AD}{AB}\)  (If two triangles are similar, then their corresponding sides are proportional)

\(\Rightarrow\frac{DE}{7.5\ cm} = \frac {2\ cm}{5\ cm} \quad(AB = AD + BD)\) 

\(\Rightarrow DE = \frac{7.5 \times 2}5 = 3\ cm\)