Correct answer is : 5
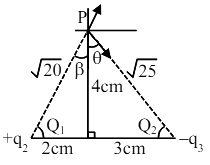
\(\frac{\mathrm{Kq}_{2}}{20} \cos \beta=\frac{\mathrm{Kq}_{3}}{25} \cos \theta\)
\(\frac{\mathrm{Kq}_{2}}{20} \frac{4}{\sqrt{20}}=\frac{\mathrm{Kq}_{3}}{25} \frac{4}{\sqrt{25}}\)
\(\frac{\mathrm{q}_{2}}{\mathrm{q}_{3}}=\frac{20}{25} \sqrt{\frac{20}{25}}=\frac{8}{5 \sqrt{\mathrm{x}}}\)
\(\Rightarrow \sqrt{\mathrm{x}}=\frac{8 \times 25 \sqrt{25}}{5 \times 20 \sqrt{20}}\)
\(\mathrm{x}=5\)