Let P(α, β, γ) be the image of the point Q(1, 6, 4) in the line x / 1 = y - 1 / 2 = z -2 / 3 Then 2α + β + γ is equal to _______ .

Question

Let \( \mathrm{P}(\alpha, \beta, \gamma)\) be the image of the point \(\mathrm{Q}(1,6,4)\) in the line \(\frac{x}{1}=\frac{y-1}{2}=\frac{z-2}{3}\). Then \(2 \alpha+\beta+\gamma\) is equal to ______.

Answer 1

Correct answer is : 11  

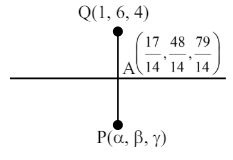
\( \frac{x}{1}=\frac{y-1}{2}=\frac{z-2}{3}\) 

\( \vec{b}=\hat{i}+2 \hat{j}+3 \hat{k} \) 

\( A(t, 2 t+1,3 t+2)\) 

\( \overrightarrow{Q A}=(t-1) i+(2 t-5) j+(3 t-2) \hat{k}\)

\( \overrightarrow{Q A} \cdot \vec{b}=0 \) 

\( (t-1)+2(2 t-5)+3(3 t-2)=0 \) 

\( 14 t=17\) 

\(\alpha=\frac{20}{14} \) 

\( \beta=\frac{12}{14}\) 

\( \gamma=\frac{102}{14} \) 

\(2 \alpha+\beta+\gamma=\frac{154}{14}=11 \text { Ans. }\)