दिया है,
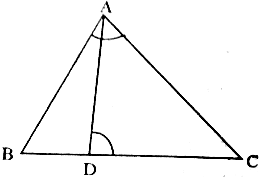
\(\angle \mathrm{ADC}=\angle \mathrm{BAC}\)
सिद्ध करना है : \(\mathrm{AC}^2=\mathrm{BC} \times \mathrm{CD}\)
प्रमाण : \(\triangle \mathrm{ABC}\) तथा \(\triangle \mathrm{ADC}\) में,
\(\angle \mathrm{C}=\angle \mathrm{C}\) उभयनिष्ठ है।
\(\angle \mathrm{BAC}=\angle \mathrm{ADC}\) दिया है।
कोण-कोण उप-प्रमेय से,
\(\triangle \mathrm{BAC} \sim \angle \mathrm{ADC}\) तो
\(\frac{\mathrm{AB}}{\mathrm{AD}}=\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{\mathrm{AC}}{\mathrm{DC}}\)
अत: \(\mathrm{AC}^2=\mathrm{BC} \times \mathrm{DC}\) सिद्ध हुआ।
