Neutral point
A neutral point is that point where the field due to magnet is completely neutralised by the horizontal component of earth’s magnetic field. Thus, at the neutral point, if B is the magnetic field due to magnet and H, the horizontal component of earth’s magnetic field, then
B = H
Let us consider the position of the neutral point for the following two positions of a magnet:
(i) When magnet is placed with its north pole towards north of the earth.
Magnetic field due to a small bar magnet by placing its north pole towards north of the earth, then plot of magnetic field of the magnet is shown in Fig.
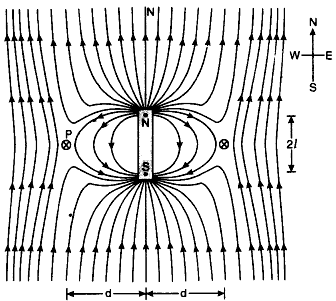
The magnetic field due to earth and that due to magnet cancel out at the two cross-marks on the equatorial line of the magnet. The normal bisector through the centre of the magnets and these positions are called neutral points. Let d be distance of each neutral point from the centre of the magnet. At neutral point, magnetic field due to the magnet is equal to magnetic field due to the earth.
∴ H = \((\frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{M}}{\left(d^2+l^2\right)^{3 / 2}})\) .............(1)
In case, the magnet is so small then l2 can be neglected as compared to d2, then
\((\frac{\mu_0}{4 \pi} \cdot \frac{\mathbf{M}}{d^3})\) = H ............(2)
Knowing d and H the magnetic dipole moment of the bar can be calculated from equation.
(ii) When magnet is placed with its south pole towards north of the earth. The plot of magnetic field of the magnet in the case will be as shown in Fig.
The neutral points he on the axial line. At a neutral point, magnetic intensity due to magnet = magnetic field due to the earth.


Knowing d, H this equation can be used to find magnetic dipole of the magnet.