Question

Establish the phase relation between voltage and current in an a.c. circuit containing resistance R and inductance L and determine the impedance of LR circuit.

Answer 1

Let an inductance L and resistance R be connected in series to a source of an alternating e.m.f. E as shown in Fig. (a).

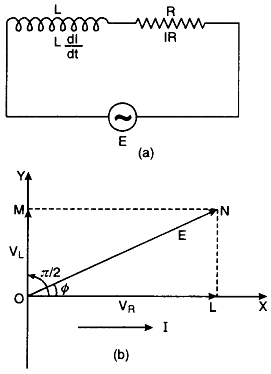
The alternating current I at all points in series circuit has the same amplitude and phase but the voltage across each element will be of different amplitude and phase.

(i) If V_R is the voltage across R, then

V_R= IR

Voltage across the resistor is in phase with current

(ii) If V_L is the voltage across, then

V_L = I X_L

Voltage across the inductor leads the current by a phase π/2.

Let us construct the phasor diagram for this circuit. A single phasor I is used to represent the current in each element and V_R and V_L represent voltage phasors. If V_R is represented along OX by OL, (current is also along OX) then V_L will be along OY by OM because V_L leads the current I by a phase π/2. This is graphically represented in Fig. (b).The resultant of V_R and V_R is represented by E and makes an angle Φ with current I.

From the phasor diagram, we find that

where Z_L = \(\sqrt{R^2+\omega^2 L^2}\)  is the effective opposition offered by L and R and is called impedance of LR circuit . Since Φ is the angle made by the resultant of V_R and V_R with X-axis, so from phasor diagram, we have

tan Φ = \(\frac{LN}{OL} =\frac{OM}{OL} = \frac{V_L}{V_R}\)

= \(\frac{IX_L}{IR}\)

= \(\frac{X_L}{R} = \frac{\omega L}{R}\) 

or tan Φ = \(\frac{\omega L}{R}\) ..........(2)

Equation (2) gives the phase angle Φ, by which alternating e.m.f. (voltage) leads the current in an LR-circuit.