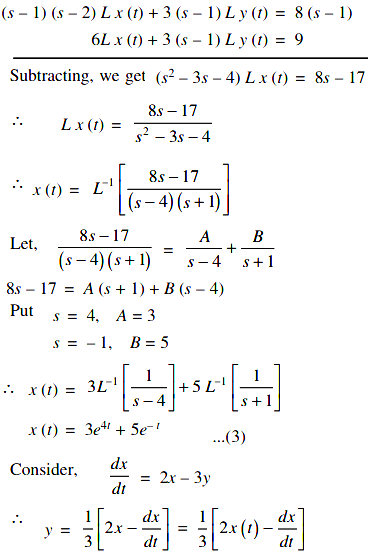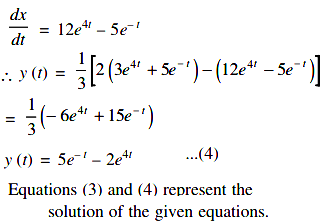Question

Solve the simultaneous equations using Laplace transforms, dx/dt = 2x – 3y, dy/dt = y – 2x subject to x(0) = 8 and y(0) = 3

Answer 1

We have,

x′ (t) – 2x (t) + 3y (t)=0

2x (t) + y′ (t) – y (t)=0

Taking Laplace transforms on both sides of these, we get

L [x′ (t)] – 2L[x (t)] + 3L[y(t)] = 0

2L [x(t)] + L[y′(t)] – L[ y(t)] = 0

i.e., sLx(t) – x (0) – 2Lx(t) + 3L y(t)=0

2Lx (t) + sLy(t) – y(0) – Ly(t)=0

Using initial values, 

Since, x(0) = 8, and y(0) = 3, we get 

(s – 2) Lx(t) + 3Ly (t) = 8 ...(1) 

2Lx(t) + (s – 1) Ly(t) = 3 ...(2) 

Solving the Eqns. (1) and (2) 

Multiplying (s – 1) in the Eqn. (1) and Multiplying 3 by (2)