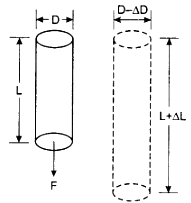
We have observed many times that stretching, applying load or applying an external force causes deformations in the dimensions of a material such as if a rubber band is stretched, the shape changes and so the dimensions. Similarly if a wire is stretched or is loaded with a mass there is change in the dimensions of the wire. The length increases but the diameter decreases and thus decreases the area of cross section of the wire. This also gives rise to two types of strains-longitudinal strain and lateral strain. Longitudinal strain is the strain produced in the direction of the applied force; whereas the strain produced in the perpendicular direction is called lateral strain.
Hence, poisson's ratio is defined as:
"The ratio of lateral strain to longitudinal strain within the elastic limit."
Suppose, the length of the wire increases from L to L + ∆L and its diameter decreases from D to D - ∆D.

The negative sign here indicates that longitudinal and lateral strains are opposite.
Poisson's ratio has no units and dimensions.
The theoretical value of possion's ratio is -1 to \(\frac{1}{2}\).
The experimental value of possion's ratio is 0 to \(\frac{1}{2}\).